Risk
Solutions
A complete risk analytics suite that transforms complex portfolios into transparent, actionable insights. From tail risk to sensitivities, stress testing, Greeks, and convexity, LumRisk gives you a unified, model-consistent view of where your risks truly come from.
CVaR Contribution
Get a transparent, position-based view of tail risk across your entire portfolio. The result is a clear breakdown of CVaR at both strategy and portfolio level, with detailed contributions by factor, sector, asset class, or any category you choose, giving you a precise understanding of where your risk truly comes from.
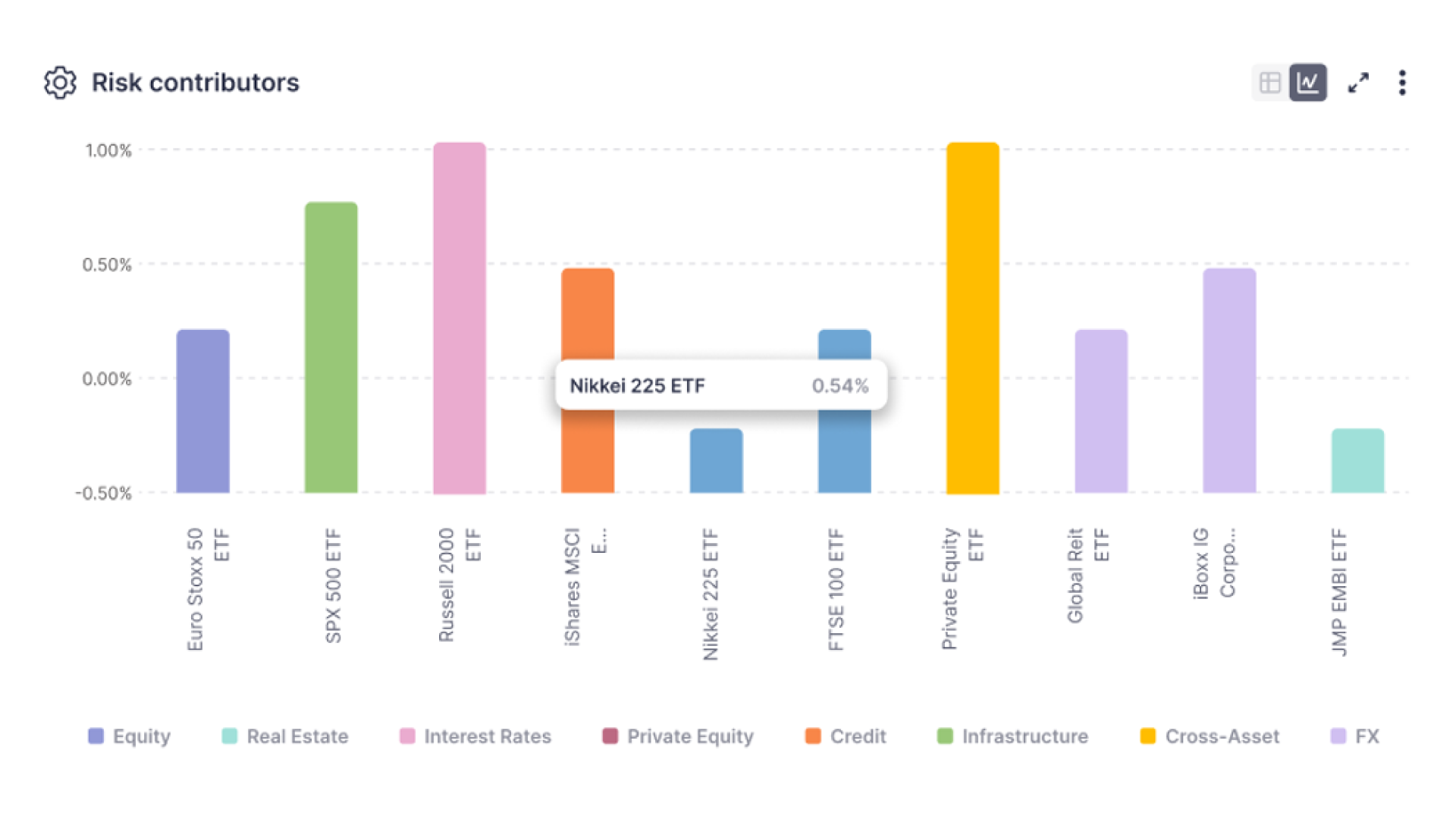
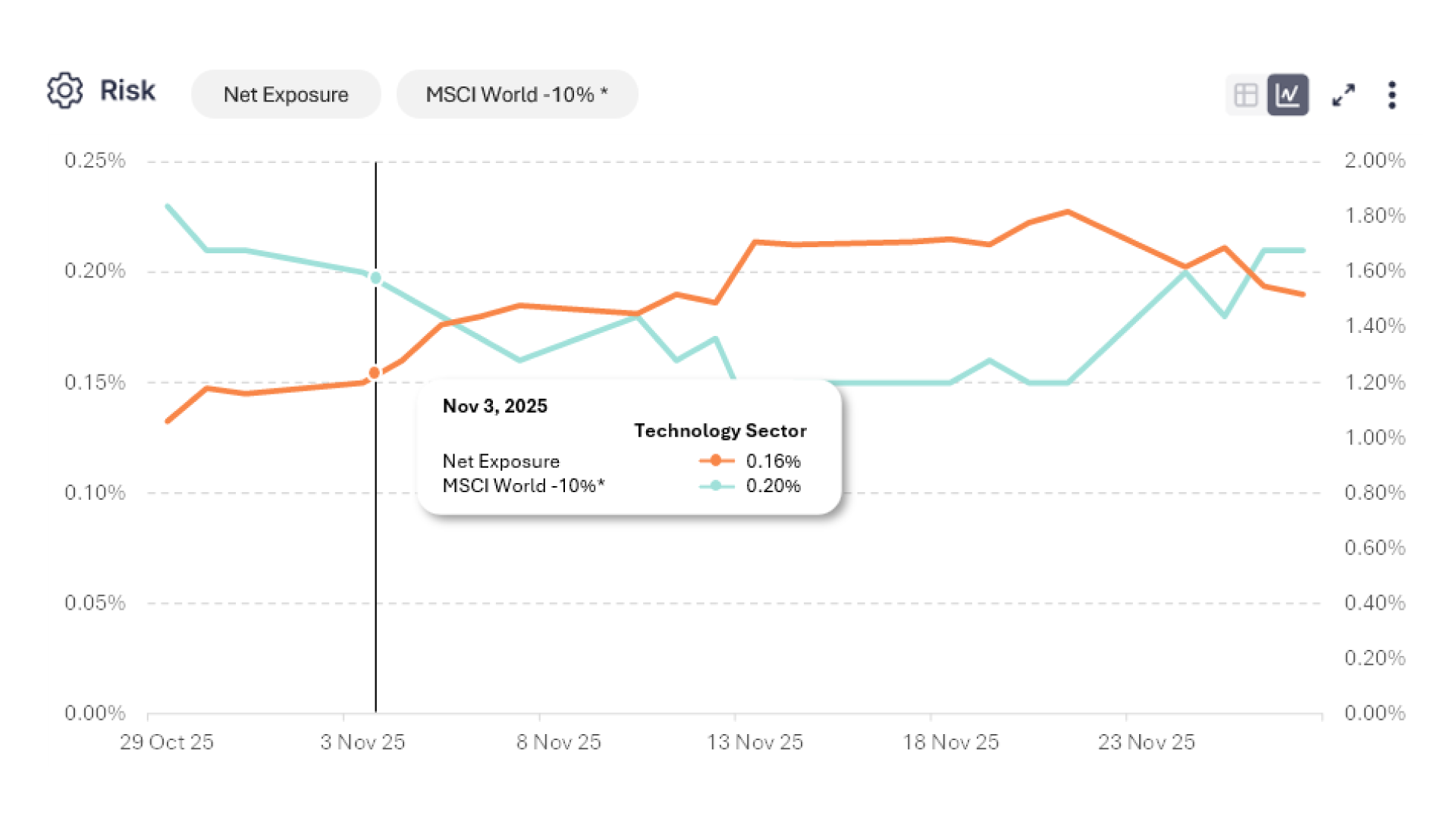
Exposures & Sensitivities
Understand how your portfolio behaves under a wide range of market environments. With more than 300 constrained and cross-asset stress tests, you can explore how shocks propagate across risk factors and uncover your portfolio’s true sensitivity profile. Full re-pricing across hundreds of scenarios provides model-consistent sensitivities for every underlying instrument, while intuitive exposure breakdowns by sector, industry, region, or custom group give you instant visibility into concentration and diversification.
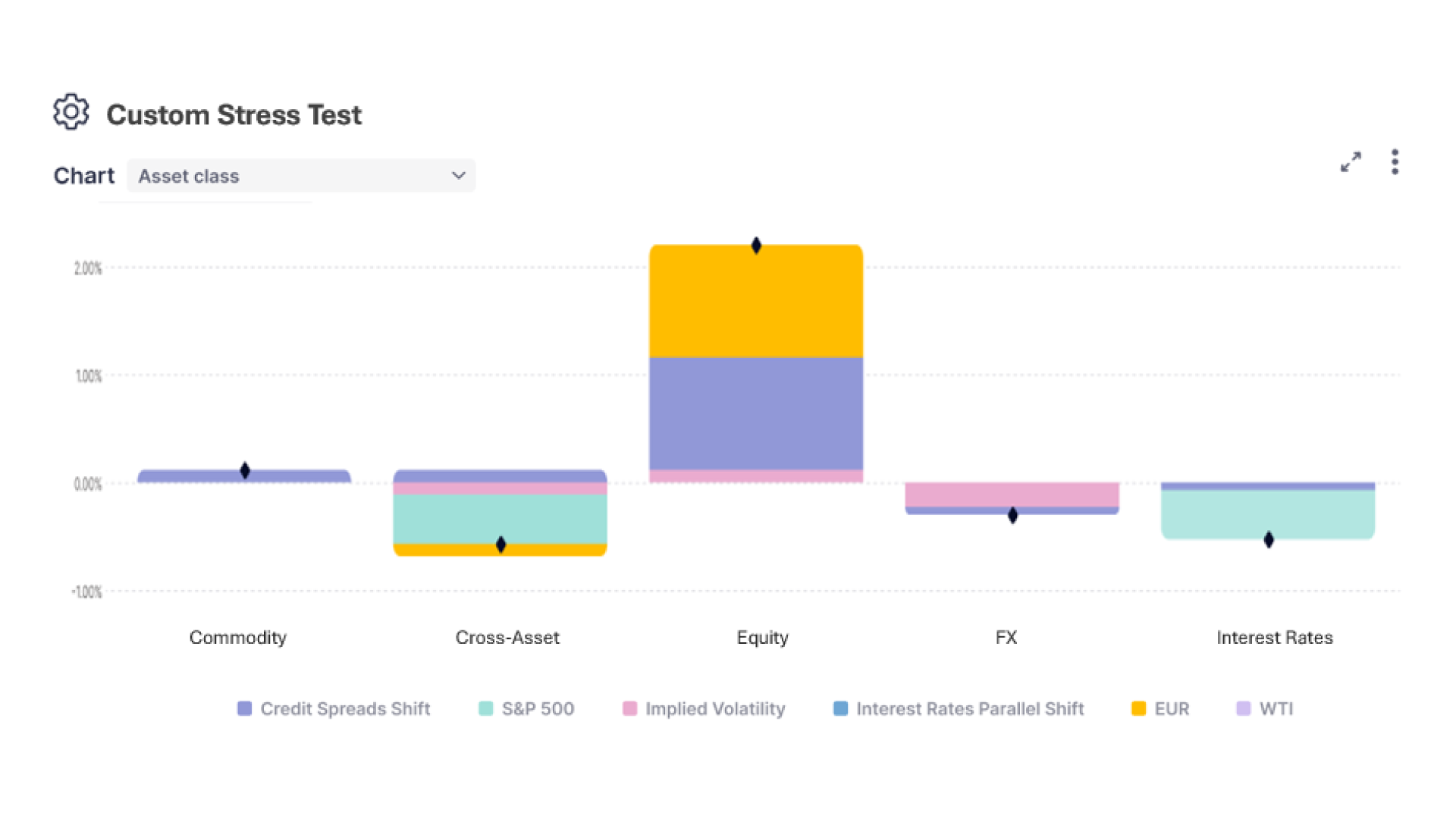
Custom Stress Tests
Create your own market scenarios by applying user-defined shocks across any combination of risk factors. These shocks propagate through the portfolio using correlation-aware dynamics, allowing you to measure the total impact of the scenario, not just isolated effects. Granular contribution analysis shows exactly how the shock spreads across positions and strategies, giving you full control to design, test, and interpret bespoke stress events in real time.
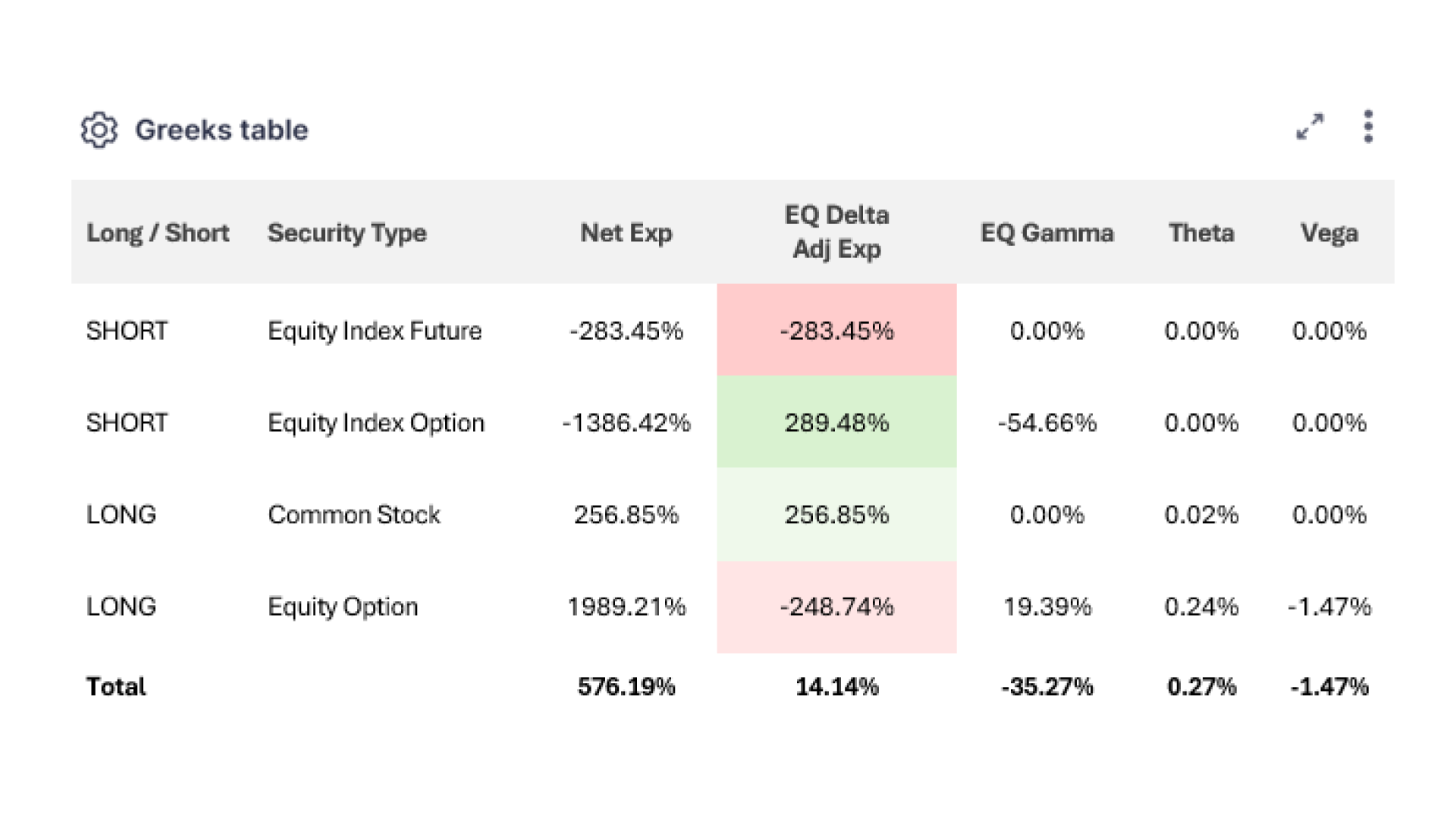
Greeks & Convexity
Obtain a clear snapshot of your portfolio’s option sensitivities at any point in time. Delta, gamma, vega, and theta are calculated consistently for every position across asset classes, providing a unified view of directional, curvature, and volatility exposure. With transparent long/short aggregation and instrument-level decomposition, you can easily identify where non-linear risks reside and how they shape your portfolio’s overall convexity profile.